Algorithms for Quantum Computing: Quantum dynamics and electronic structure
Representative publications
85 Quantum nuclear dynamics on a distributed set of ion-trap quantum computing systems
Anurag Dwivedi, A. J. Rasmusson, Philip Richerme, Srinivasan S. Iyengar, "Quantum nuclear dynamics on a distributed set of ion-trap quantum computing systems", J. Am. Chem. Soc. ASAP (2024).
84 Resource optimization for quantum dynamics with tensor networks: Quantum and Classical Algorithms
A. Dwivedi, M. A. Lopez-Ruiz, and S. S. Iyengar, “Resource optimization for quantum dynamics with tensor networks: Quantum and Classical Algorithms” J. Phys. Chem. A, 128 , 6774 (2024).
82 A reformulation of all ONIOM-type molecular fragmentation approaches using graph theory-based projection operators: Applications to dynamics, molecular potential surfaces, and machine learning and quantum computing
S. S. Iyengar, Timothy C. Ricard, Xiao Zhu, “A reformulation of all ONIOM-type molecular fragmentation approaches using graph theory-based projection operators: Applications to dynamics, molecular potential surfaces, and machine learning and quantum computing” J. Phys. Chem. A, ASAP (2023). J. Phys. Chem. A 128, 466 (2024).
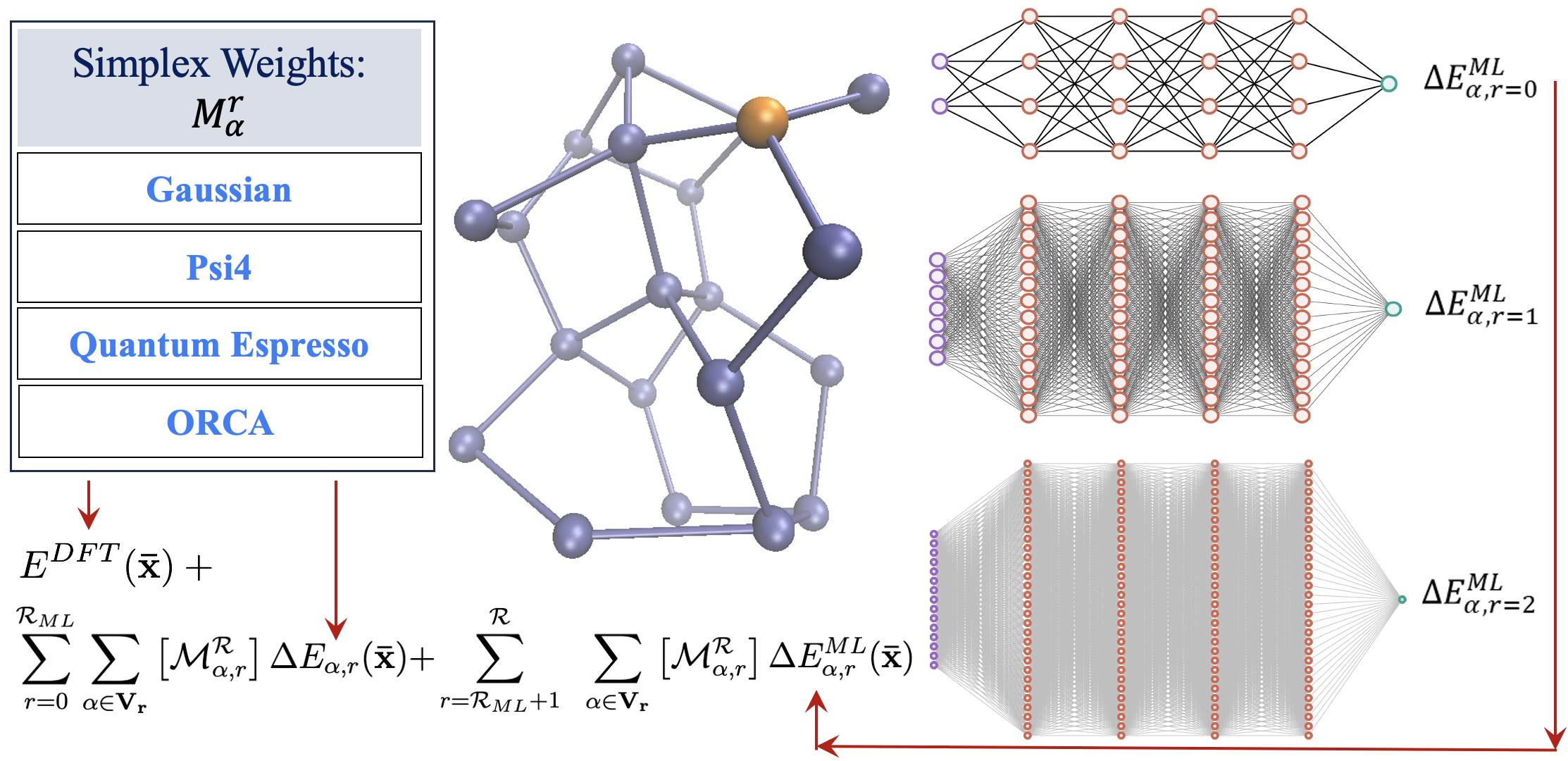Summary: We present a graph-theory-based reformulation of all ONIOM-based molecular fragmentation methods. We discuss applications to (a) accurate post-Hartree–Fock AIMD that can be conducted at DFT cost for medium-sized systems, (b) hybrid DFT condensed-phase studies at the cost of pure density functionals, (c) reduced cost on-the-fly large basis gas-phase AIMD and condensed-phase studies, (d) post-Hartree–Fock-level potential surfaces at DFT cost to obtain quantum nuclear effects, and (e) novel transfer machine learning protocols derived from these measures. Additionally, in previous work, the unifying strategy discussed here has been used to construct new quantum computing algorithms. Thus, we conclude that this reformulation is robust and accurate.
80 Graph-|Q⟩⟨C|: A Quantum algorithm with Reduced quantum circuit depth for electronic structure
S. S. Iyengar, Juncheng (Harry) Zhang, Timothy C. Ricard and Debadrita Saha, “Graph-|Q⟩⟨C|: A Quantum algorithm with Reduced quantum circuit depth for electronic structure”, J. Phys. Chem. A, 127, 9334 (2023).
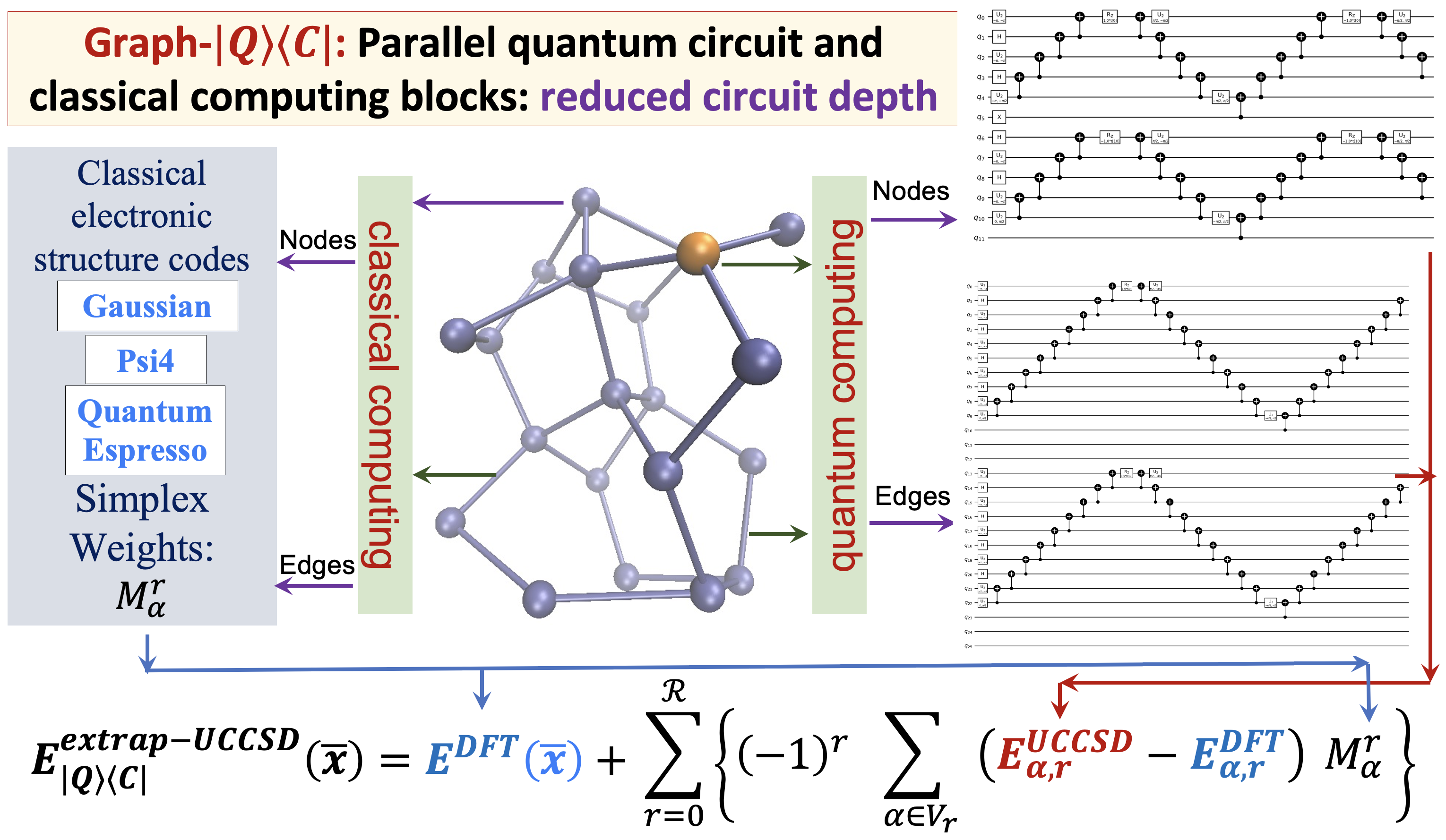Summary: The accurate determination of chemical properties is known to have a critical impact on multiple fundamental chemical problems but is deeply hindered by the steep algebraic scaling of electron correlation calculations and the exponential scaling of quantum nuclear dynamics. With the advent of new quantum computing hardware and associated developments in creating new paradigms for quantum software, this avenue has been recognized as perhaps one way to address exponentially complex challenges in quantum chemistry and molecular dynamics. In this paper, we discuss a new approach to drastically reduce the quantum circuit depth (by several orders of magnitude) and help improve the accuracy in the quantum computation of electron correlation energies for large molecular systems. The method is derived from a graph-theoretic approach to molecular fragmentation and enables us to create a family of projection operators that decompose quantum circuits into separate unitary processes. Some of these processes can be treated on quantum hardware and others on classical hardware in a completely asynchronous and parallel fashion. Numerical benchmarks are provided through the computation of unitary coupled-cluster singles and doubles (UCCSD) energies for medium-sized protonated and neutral water clusters using the new quantum algorithms presented here.
79 A Synthesis of Hidden Subgroup Quantum Algorithms and Quantum Chemical Dynamics
S. S. Iyengar, A. Kumar, Debadrita Saha, and A. Sabry, “A Synthesis of Hidden Subgroup Quantum Algorithms and Quantum Chemical Dynamics”. J. Chem. Theory and Comput. 19, 6082 (2023).
Summary: We describe a general formalism for quantum dynamics and show how this formalism subsumes several quantum algorithms including the Deutsch, Deutsch-Jozsa, Bernstein-Vazirani, Simon, and Shor algorithms as well as the conventional approach to quantum dynamics based on tensor networks. The common framework exposes similarities among quantum algorithms and natural quantum phenomena: we illustrate this connection by showing how the correlated behavior of protons in water wire systems that are common in many biological and materials systems parallels the structure of Shor's algorithm.
78 Quantum Computing with Dartboards
Ishaan Ganti , and S. S. Iyengar, “Quantum Computing with Dartboards” J. Phys. Chem. A, 127 , 7853 (2023).
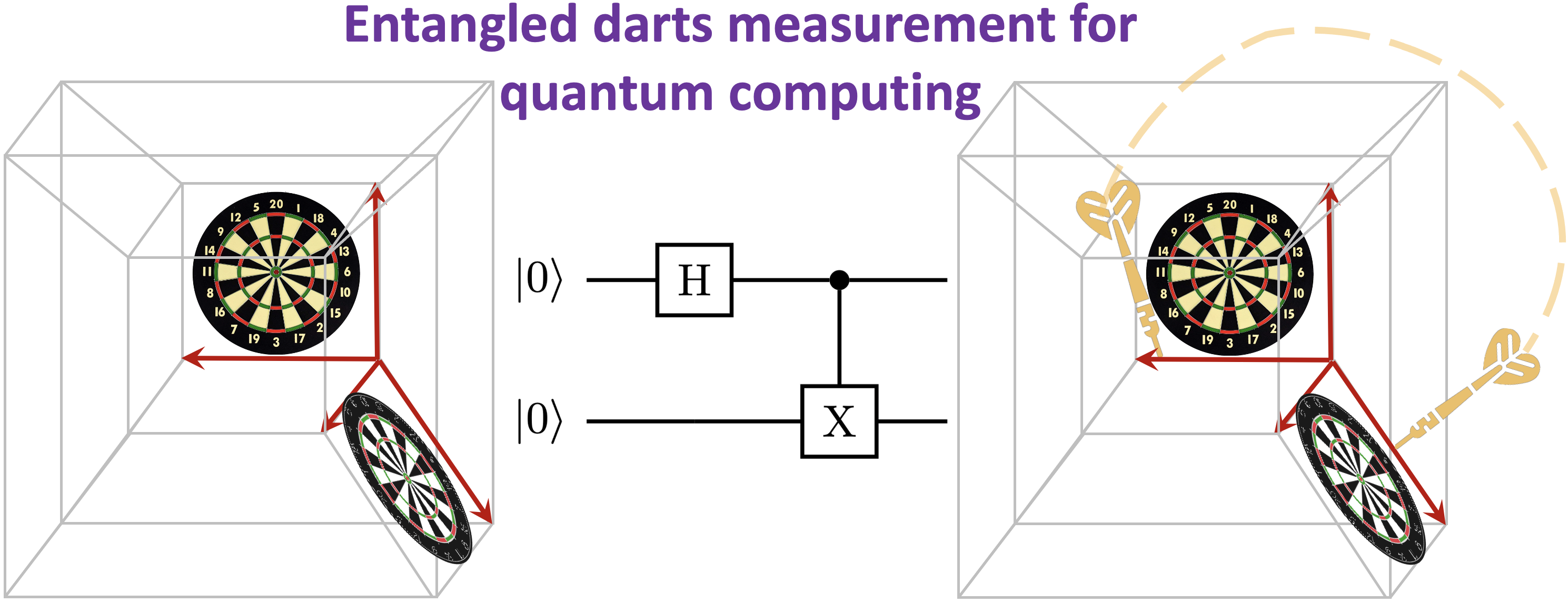Summary: We present a physically appealing and elegant picture for quantum computing using rules constructed for a game of darts. A dartboard is used to represent the state space in quantum mechanics and the act of throwing the dart is shown to have close similarities to the concept of measurement, or collapse of the wavefunction in quantum mechanics. The analogy is constructed in arbitrary dimensional spaces, that is using arbitrary dimensional dartboards, and for for such arbitrary spaces this also provides us a ``visual'' description of uncertainty. Finally, connections of qubits and quantum computing algorithms is also made opening the possibility to construct analogies between quantum algorithms and coupled dart-throw competitions.
77 Quantum Computation of Hydrogen Bond Dynamics and Vibrational Spectra
P. Richerme, Melissa C. Revelle, Debadrita Saha, Miguel Angel Lopez-Ruiz, Anurag Dwivedi, Sam A. Norrell, Christopher G. Yale, Daniel Lobser, Ashlyn D. Burch, Susan M. Clark, J. M. Smith, A. Sabry, and S. S. Iyengar “Quantum Computation of Hydrogen Bond Dynamics and Vibrational Spectra”. J. Phys. Chem. Lett. 14, 7256 (2023).
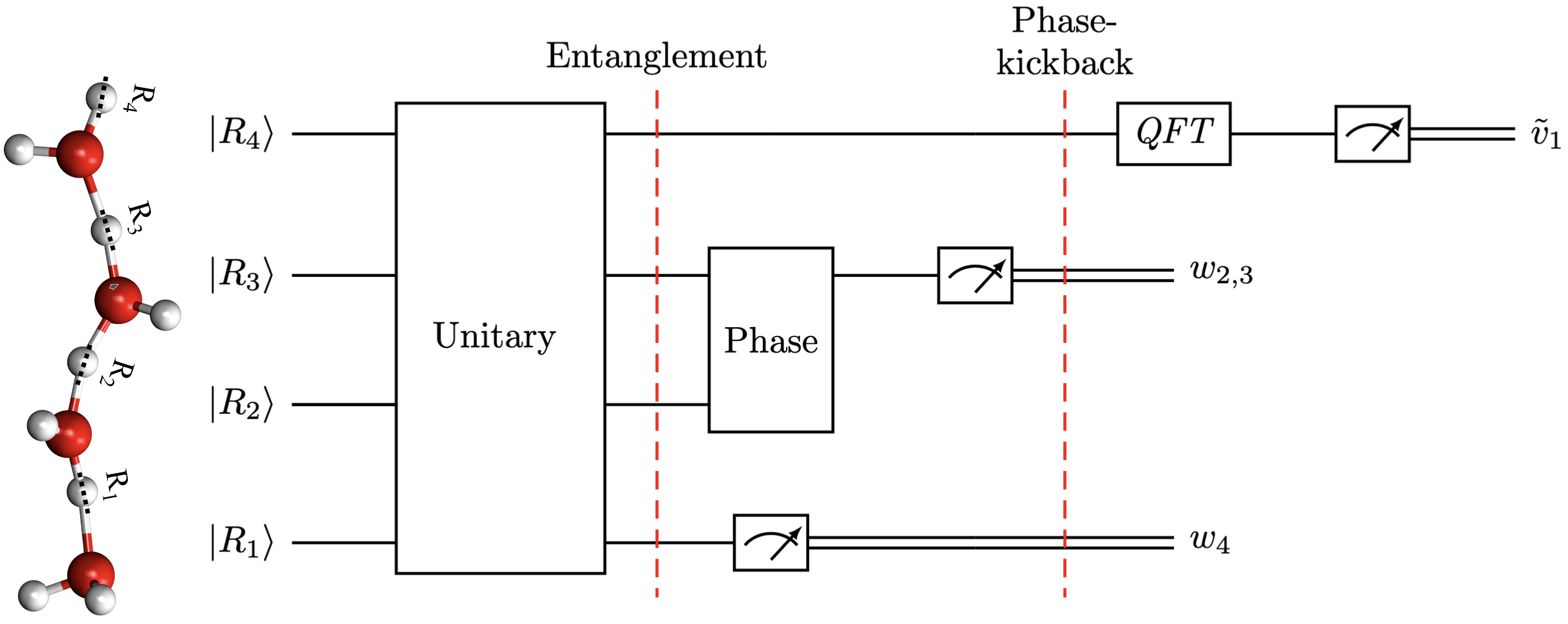
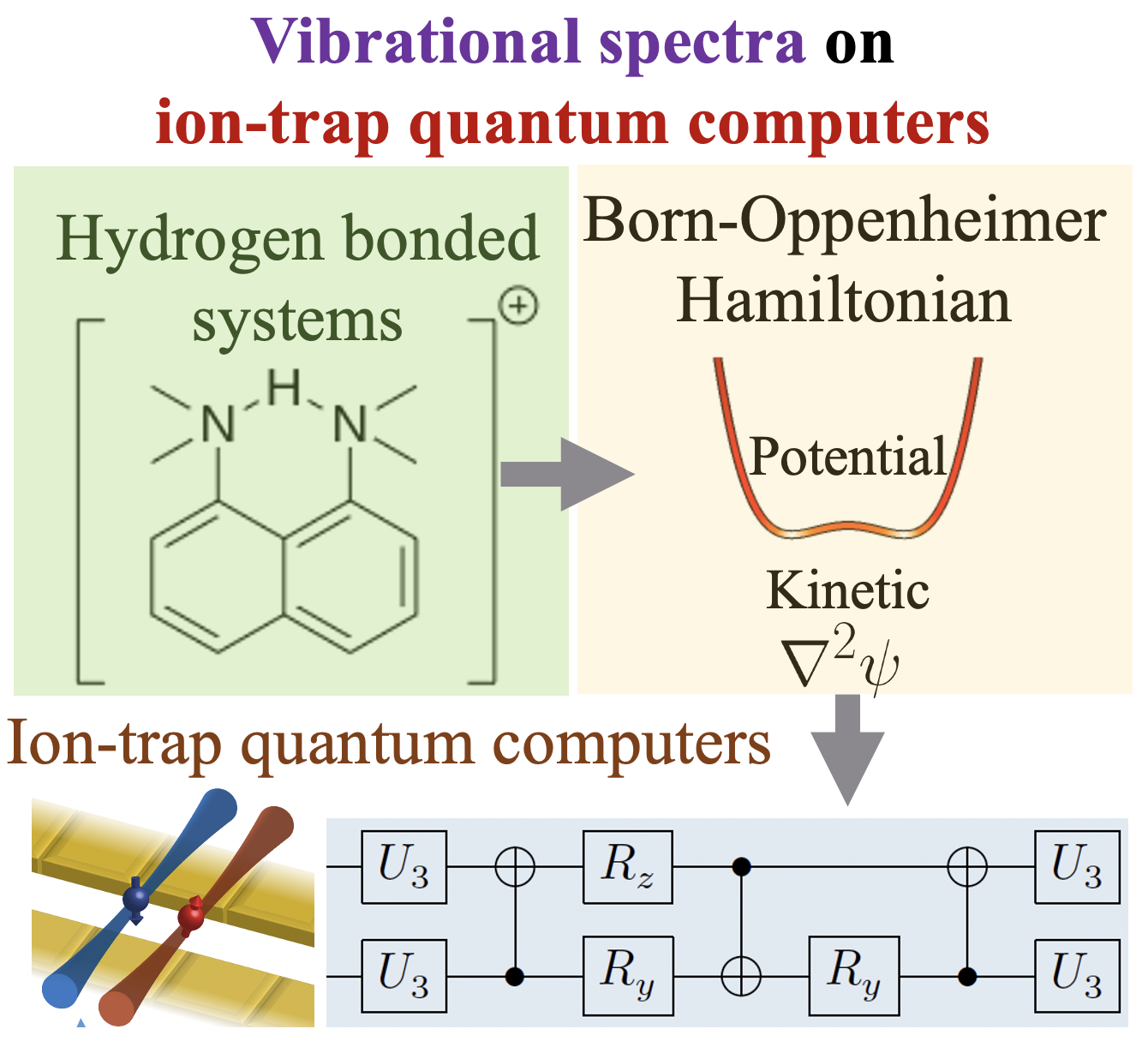Summary: Calculating observable properties of chemical systems is often classically intractable and widely viewed as a promising application of quantum information processing. Here, we introduce a new framework for solving generic quantum chemical dynamics problems using quantum logic. We experimentally demonstrate a proof-of-principle instance of our method using the QSCOUT ion-trap quantum computer, where we experimentally drive the ion-trap system to emulate the quantum wavepacket dynamics corresponding to the shared-proton within an anharmonic hydrogen bonded system. Following the experimental creation and propagation of the shared-proton wavepacket on the ion-trap, we extract measurement observables such as its time-dependent spatial projection and its characteristic vibrational frequencies to spectroscopicaccuracy (3.3 cm−1 wavenumbers, corresponding to >99.9% fidelity). Our approach introduces a new paradigm for studying the chemical dynamics and vibrational spectra of molecules and opens the possibility to describe the behavior of complex molecular processes with unprecedented accuracy.
76 Quantum algorithms for the study of electronic structure and molecular dynamics: Novel computational protocols
S. S. Iyengar, Debadrita Saha, Anurag Dwivedi, Miguel Angel Lopez-Ruiz, Anup Kumar, Juncheng (Harry) Zhang, Timothy C. Ricard, Philip Richerme Amr Sabry “Quantum algorithms for the study of electronic structure and molecular dynamics: Novel computational protocols” In Comprehensive Computational Chemistry. In Press. (2023)
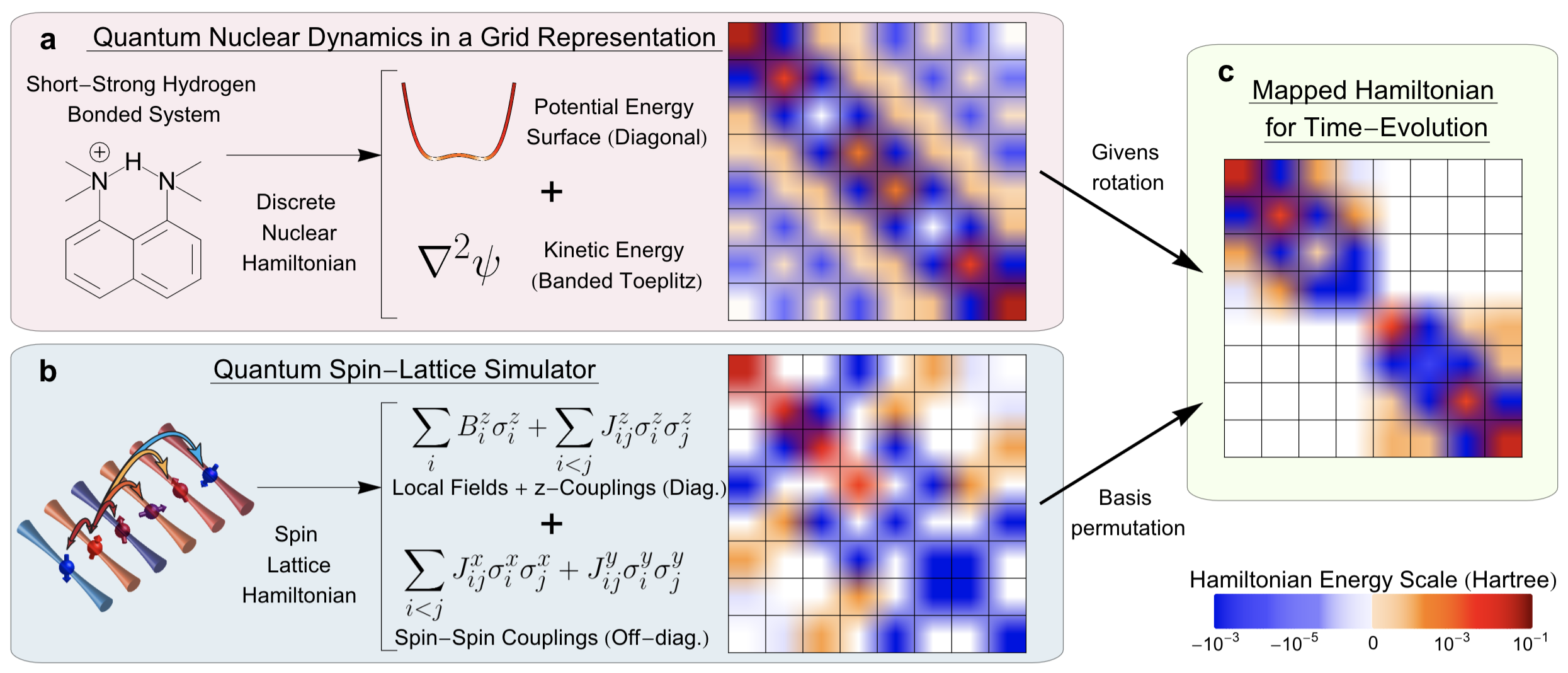
Summary: The accurate computational determination of chemical, materials, biological, and atmospheric properties has critical impact on a wide range of health and environmental problems, but is deeply limited by the computational scaling of quantum-mechanical methods. The complexity of quantum-chemical studies arises from the steep algebraic scaling of electron correlation methods, and the exponential scaling in studying nuclear dynamics and molecular flexibility. In this article we provide an overview of the challenges involved in performing accurate post-Hartree-Fock electronic structure and quantum nuclear dynamics calculations on quantum hardware. For electronic structure, we present a procedure to drastically reduce the depth of quantum circuits and improve the accuracy of results in computing post-Hartree-Fock electronic structure energies for large molecular systems. The method is based on molecular fragmentation where a molecular system is divided into overlapping fragments through a graph theoretic procedure. This allows us to create a set of projection operators that decompose the unitary evolution of the full system into separate sets of unitary processes, some of which can be treated on quantum hardware and others on classical hardware. Thus, we develop a procedure for electronic structure that can be asynchronously spawned onto a potentially large ensemble of classical and quantum hardware systems. We also discuss a framework which allows for the solution of quantum chemical nuclear dynamics by mapping these to quantum spin-lattice simulators. This mapping procedure allows us to determine the local fields and spin-spin couplings needed to identically match the molecular and spin-lattice Hamiltonians and hence the resultant dynamics.
75 Exploiting analogies between Boltzmann machines and Feynman path integrals
S. S. Iyengar, and S. Kais “Exploiting analogies between Boltzmann machines and Feynman path integrals”. J. Chem. Theory and Comput. 19, 2446 (2023).
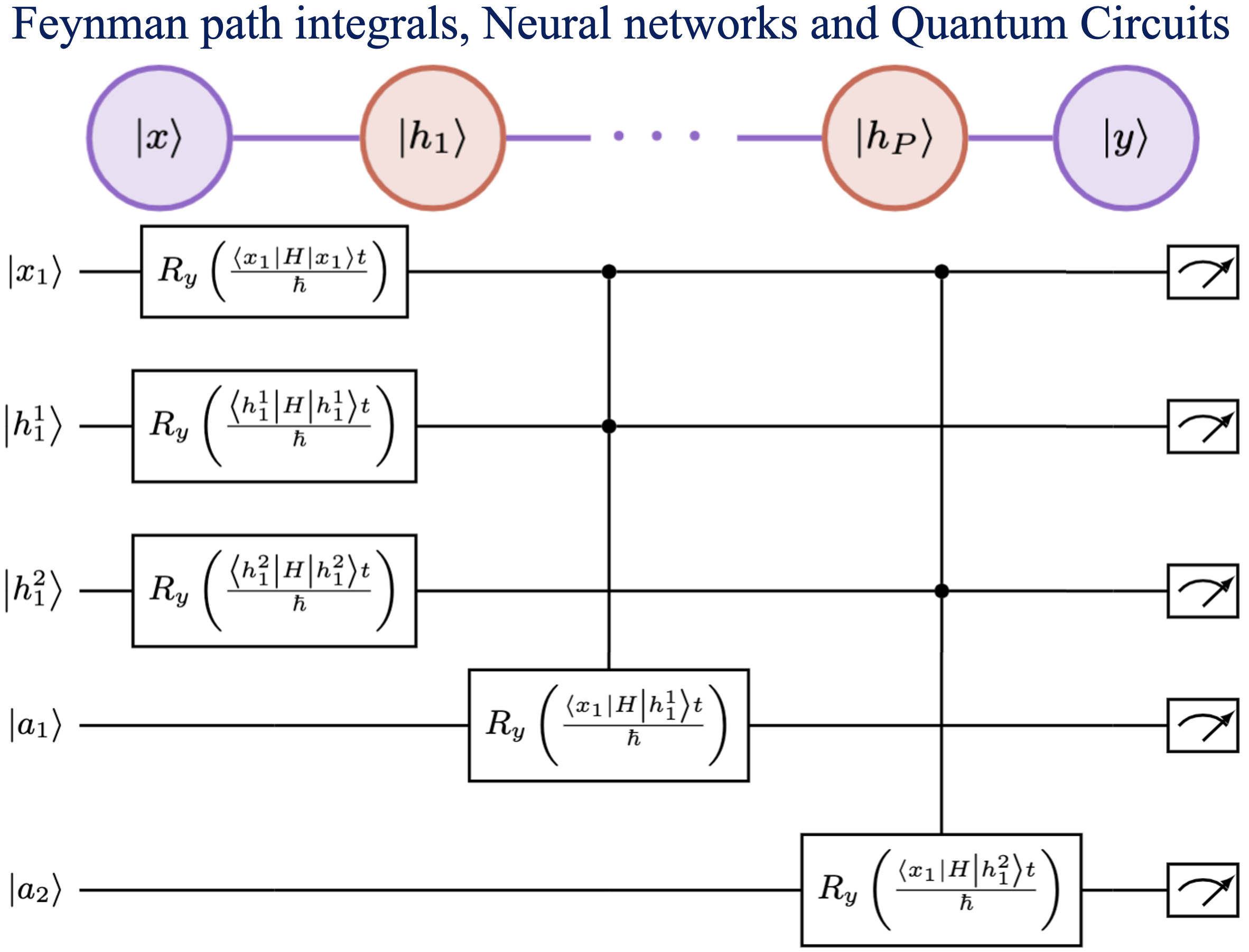Summary: Machine learning has had a significant impact on multiple areas of science, technology, health, and computer and information sciences. Through the advent of quantum computing, quantum machine learning has developed as a new and important avenue for the study of complex learning problems. Yet there is substantial debate and uncertainty in regard to the foundations of machine learning. Here, we provide a detailed exposition of the mathematical connections between a general machine learning approach called Boltzmann machines and Feynman’s description of quantum and statistical mechanics. In Feynman’s description, quantum phenomena arise from an elegant, weighted sum over (or superposition of) paths. Our analysis shows that Boltzmann machines and neural networks have a similar mathematical structure. This allows the interpretation that the hidden layers in Boltzmann machines and neural networks are discrete versions of path elements and allows a path integral interpretation of machine learning similar to that in quantum and statistical mechanics. Since Feynman paths are a natural and elegant depiction of interference phenomena and the superposition principle germane to quantum mechanics, this analysis allows us to interpret the goal in machine learning as finding an appropriate combination of paths, and accumulated path-weights, through a network, that cumulatively captures the correct properties of an x-to-y map for a given mathematical problem. We are forced to conclude that neural networks are naturally related to Feynman path-integrals and hence may present one avenue to be considered as quantum problems. Consequently, we provide general quantum circuit models applicable to both Boltzmann machines and Feynman path integrals.
74 Graph-theoretic Molecular fragmentation for potential surfaces leads naturally to a tensor network form and allows accurate and efficient quantum nuclear dynamics
A. Kumar, N. DeGregorio T. C. Ricard, and S. S. Iyengar, “Graph-theoretic Molecular fragmentation for potential surfaces leads naturally to a tensor network form and allows accurate and efficient quantum nuclear dynamics”. J. Chem. Theory and Comput. 18, 7243 (2022).
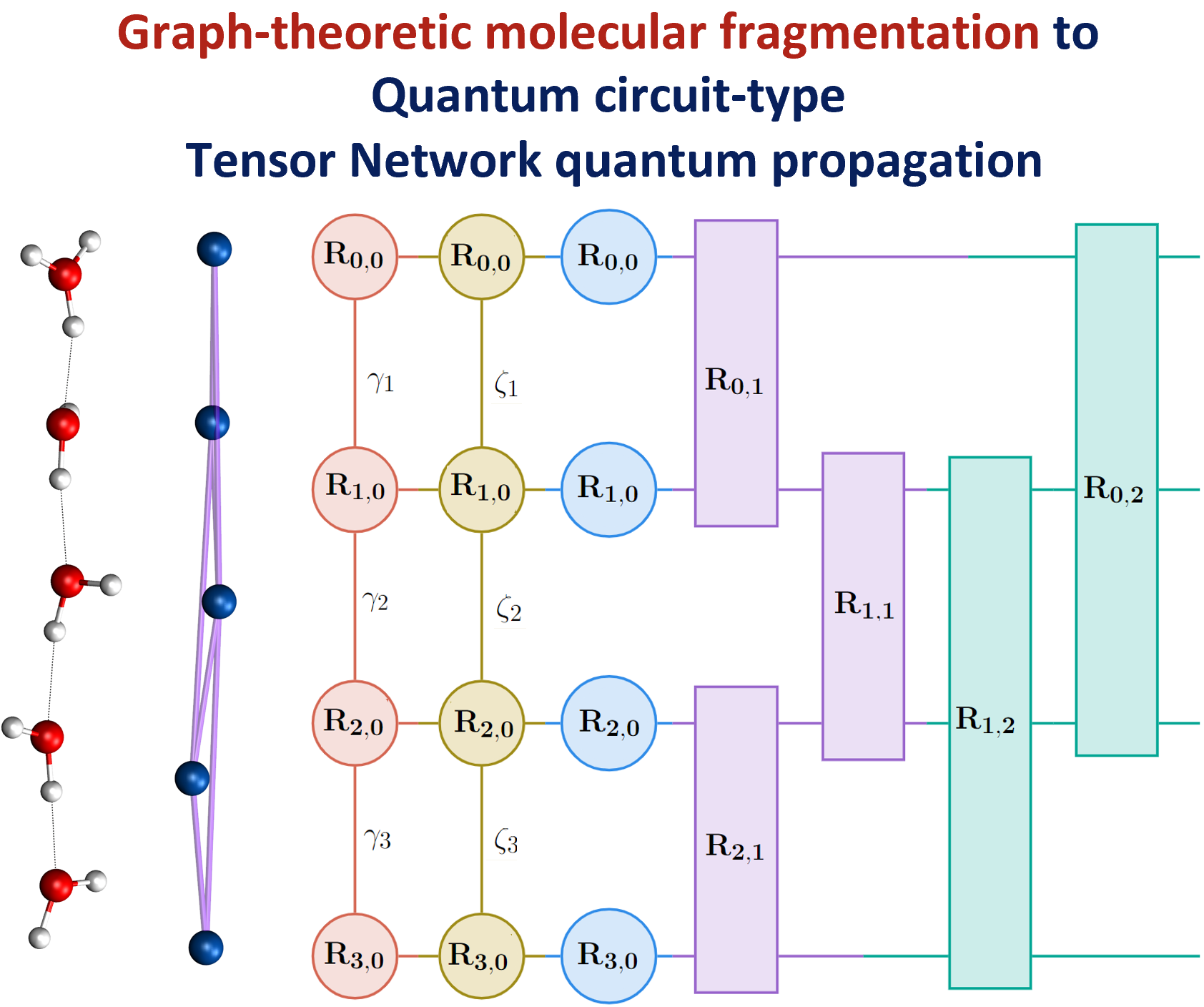Summary: Molecular fragmentation methods have revolutionized quantum chemistry. Here, we use a graph-theoretically generated molecular fragmentation method, to obtain accurate and efficient representations for multidimensional potential energy surfaces and the quantum time-evolution operator, which plays a critical role in quantum chemical dynamics. In doing so, we find that the graph-theoretic fragmentation approach naturally reduces the potential portion of the time-evolution operator into a tensor network that contains a stream of coupled lower-dimensional propagation steps to potentially achieve quantum dynamics with reduced complexity. Furthermore, the fragmentation approach used here has previously been shown to allow accurate and efficient computation of post- Hartree−Fock electronic potential energy surfaces, which in many cases has been shown to be at density functional theory cost. Thus, by combining the advantages of molecular fragmentation with the tensor network formalism, the approach yields an on-the-fly quantum dynamics scheme where both the electronic potential calculation and nuclear propagation portion are enormously simplified through a single stroke. The method is demonstrated by computing approximations to the propagator and to potential surfaces for a set of coupled nuclear dimensions within a protonated water wire problem exhibiting the Grotthuss mechanism of proton transport. In all cases, our approach has been shown to reduce the complexity of representing the quantum propagator, and by extension action of the propagator on an initial wavepacket, by several orders, with minimal loss in accuracy.
72 Graph-|Q⟩⟨C|, a Graph-Based Quantum/Classical Algorithm for Efficient Electronic Structure on Hybrid Quantum/Classical Hardware Systems: Improved Quantum Circuit Depth Performance
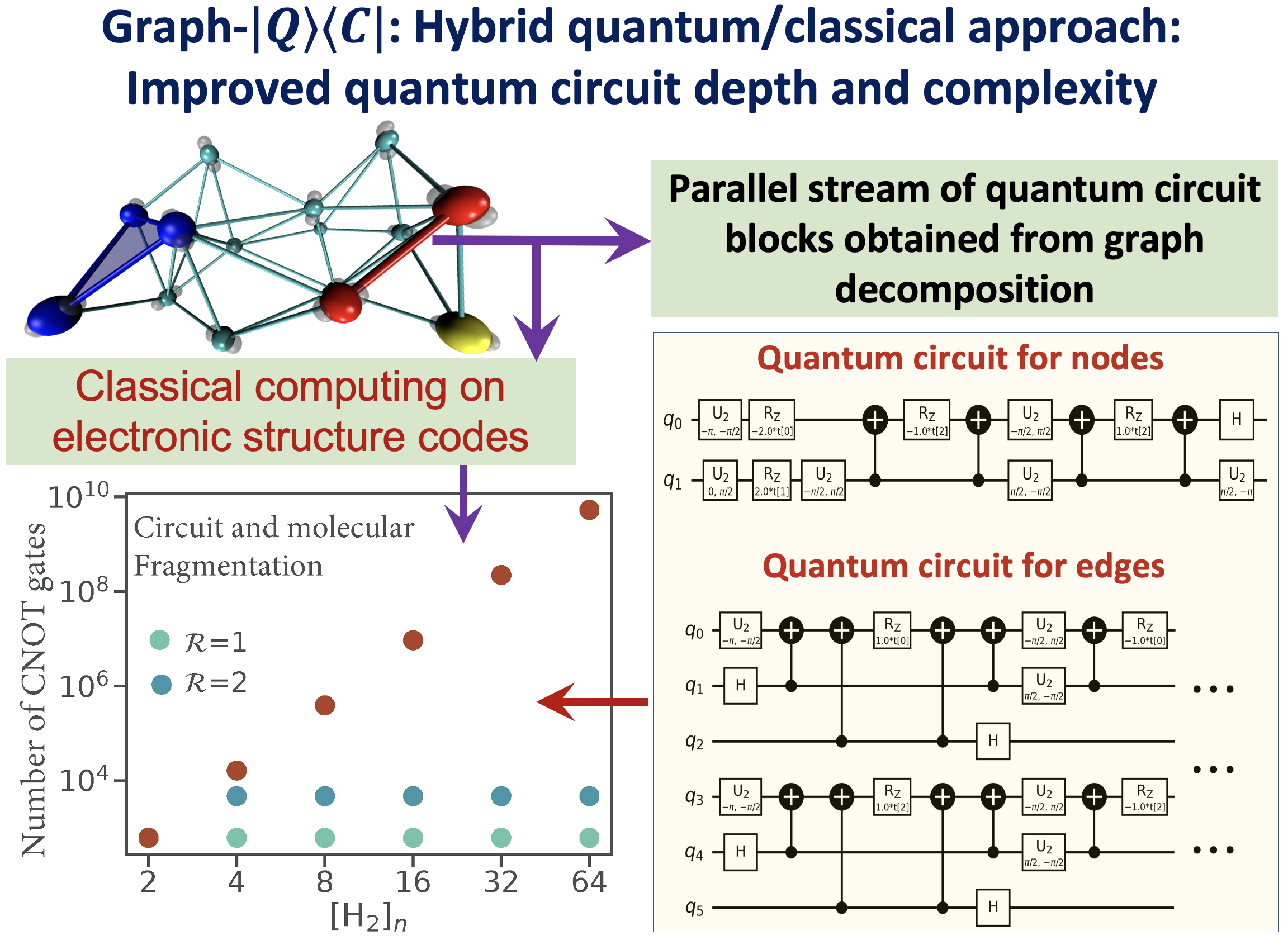Juncheng Harry Zhang, and Srinivasan S. Iyengar, J. Chem. Theory and Comput. 18, 2885 (2022).
Summary: Recently, multiple quantum computing technologies have emerged as potential alternative computational platforms to address complex computational challenges. Additionally, algorithms to approximate electron correlation problems, for small molecular systems, and quantum nuclear dynamics problems have been implemented on quantum hardware devices. However, application of standard quantum circuit models to treat electronic structure problems leads to a rapid increase in the circuit depth and the number of quantum gates. This contributes greatly to the accumulated error during quantum propagation. This paper outlines a new hybrid quantum+classical algorithm based on a graph-theoretic approach to molecular fragmentation and is geared toward performing electron correlation calculations, potentially on an ensemble of quantum and classical hardware systems. The algorithm studied here is referred to as the “Graph-|Q⟩⟨C|” algorithm since it contains an independent set of classical and quantum algorithmic components inside a single umbrella. That is, the overall computational workload is partitioned, through graph theory based on computational complexity analysis, into (a) classical computing sections that are carried out on traditional classical electronic structure packages, and (b) quantum computing sections that are carried out using quantum circuit models. Furthermore, the Graph-|Q⟩⟨C| algorithm is quantum hardware-agnostic and is developed with the goal to be implemented on all quantum hardware technologies, and, in fact, is designed to be used on an ensemble of such quantum hardware systems for any given calculation. In essence, our Graph-|Q⟩⟨C| algorithm yields a new approach that reduces the required quantum circuit depth, the number of quantum gates, and the number of CNOT gates (by several orders of magnitude) that contribute to error accumulation, through a graph-theory-based projection operator formalism. Thus, given this reduction, our algorithm, potentially improves the quantum algorithmic efficiency, provides a new avenue for quantum resource management, and also reduces the accumulation of errors during the demonstrated electronic structure calculations on quantum hardware. Given the limitations of quantum circuit gate fidelities within the gate model, this algorithm, we expect, will become a central piece in the quantum/classical computing of chemical systems.
71 Mapping quantum chemical dynamics problems to spin-lattice simulators
Debadrita Saha, Srinivasan S. Iyengar, Philip Richerme, Jeremy M. Smith, and Amr Sabry, J. Chem. Theory and Comput. 17, 6713 (2021).
Summary: The accurate computational determination of chemical, materials, biological, and atmospheric properties has critical impact on a wide range of health and environmental problems, but is deeply limited by the computational scaling of quantum-mechanical methods. The complexity of quantum-chemical studies arises from the steep algebraic scaling of electron correlation methods, and the exponential scaling in studying nuclear dynamics and molecular flexibility. To date, efforts to apply quantum hardware to such quantum chemistry problems have focused primarily on electron correlation. Here, we provide a framework which allows for the solution of quantum chemical nuclear dynamics by mapping these to quantum spin-lattice simulators.
37 Analysis of Hydrogen Tunneling in an Enzyme Active Site Using von Neumann Measurements
I. Sumner and S. S. Iyengar, "Analysis of Hydrogen Tunneling in an Enzyme Active Site Using von Neumann Measurements" Journal of Chemical Theory and Computation 6 , 1698 (2010).
The College of Arts