New computational methods for dynamics of nuclei and electrons
Potential energy surfaces are critical to determine dynamical properties, including reactivity as well as ensemble averages. However, the accurate determination of potential surfaces is compounded by (a) the (steeply algebraic) computational complexity of quantum mechanical calculations, and (b) the number of such calculations, which generally grows exponentially with system size. We tackle both problems using information theoretic measures and graph theoretic methods. These methods facilitate the study of complex phenomena in biological and atmospheric processes.
We have introduced methods that accurately compute quantum dynamical effects in a subsystem while simultaneously handling the motion of the surrounding atoms and changes in electronic structure, on-the-fly. The approach is quantum-classical, that is combines quantum mechanics and classical mechanics, and involves the synergy between a time-dependent quantum wave-packet description and ab initio molecule dynamics. As a result, the approach is called quantum-wave-packet {\em ab initio} molecular dynamics and abbreviated as QWAIMD. The approach allows a massively parallel implementation; computational treatment of simultaneous dynamics of electrons and nuclei in medium sized chemical systems can now be treated over 100s of computer processors leading to an efficient computational methodology. Furthermore, our approach allows the flexibility to treat a subset of the nuclei in a quantum mechanical fashion while simultaneously studying the dynamical evolution of the electrons with the majority of nuclei treated in a classical fashion. The links at the end of this page provide a list of publications with further details on this formalism. Also click a powerpoint presentation that describes QWAIMD may be found here.
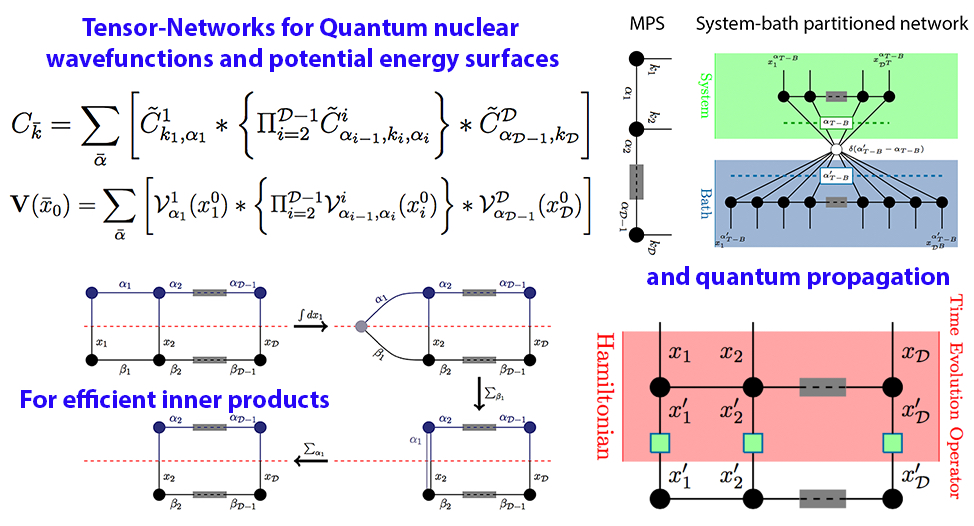
More recently, we have begun to generalize this process by introducing an approach to reduce the computational complexity and storage pertaining to quantum nuclear wave functions and potential energy surfaces. The method utilizes tensor networks. A tensor network may be thought of as a graph, but where the elements of the graphs such as nodes and edges are also thermselves matrices and higher order tensors. Using these methods drastically reduces the overall storage and computational cost and this is illustrated in the parallax graphic shown here with more details in the publitcaions below.
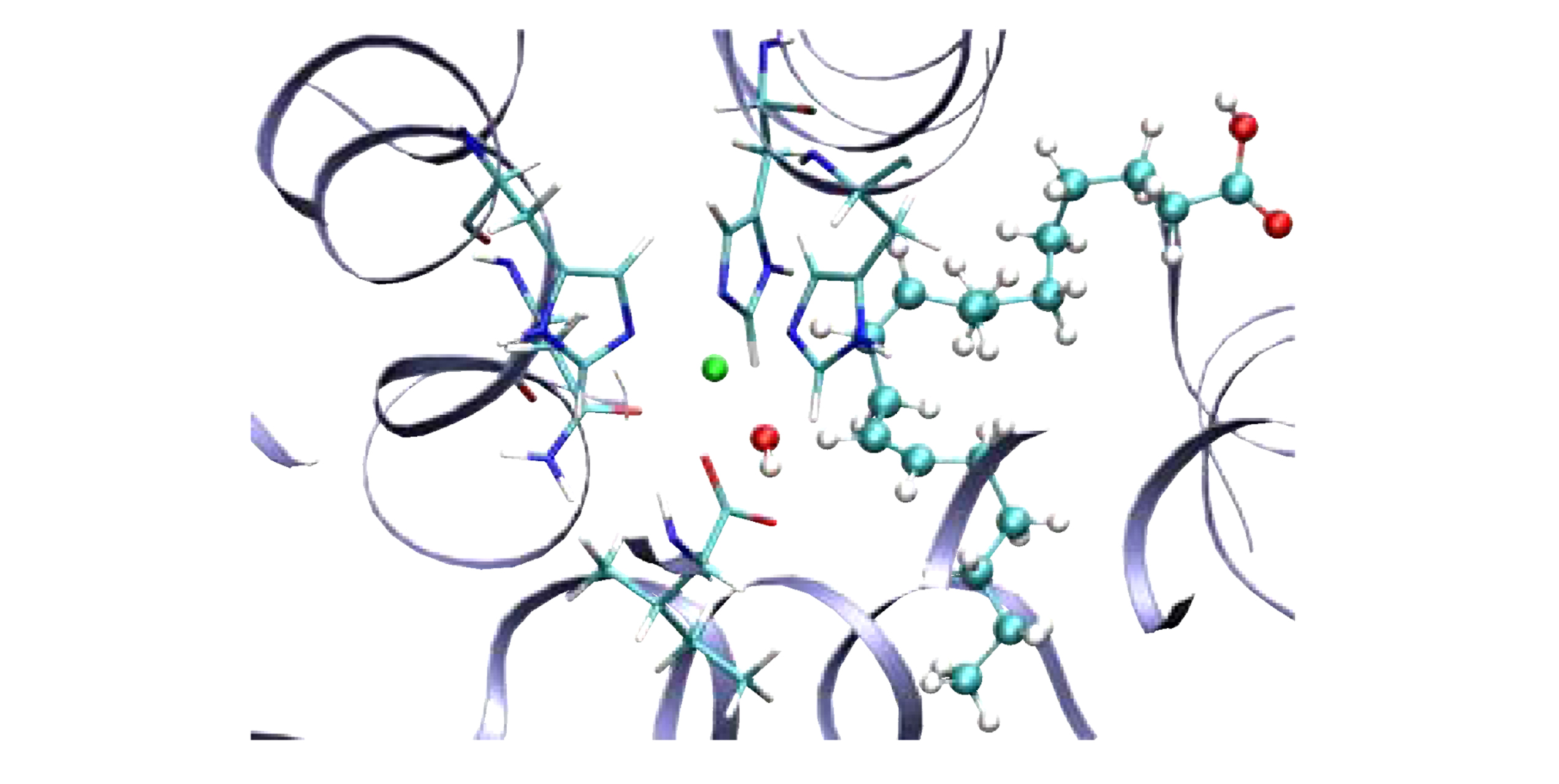
Why would one want to treat “some nuclei using quantum mechanics”? It turns out that this problem is of relevance in many biological enzyme problems and also in atmospheric chemical problems, the study of which we are now actively pursuing. As an example, of our current study, the figure on the left represents the active site of the enzyme “lipoxygenase” where the quantum dynamical nature of a transferring hydrogen atom dictates the kinetics. Such interesting chemistry is also found in many atmospheric chemical problems as a result we are currently applying this methodology to problems in biological chemistry and atmospheric chemistry. The specific studies conducted on biological systems may be found here.
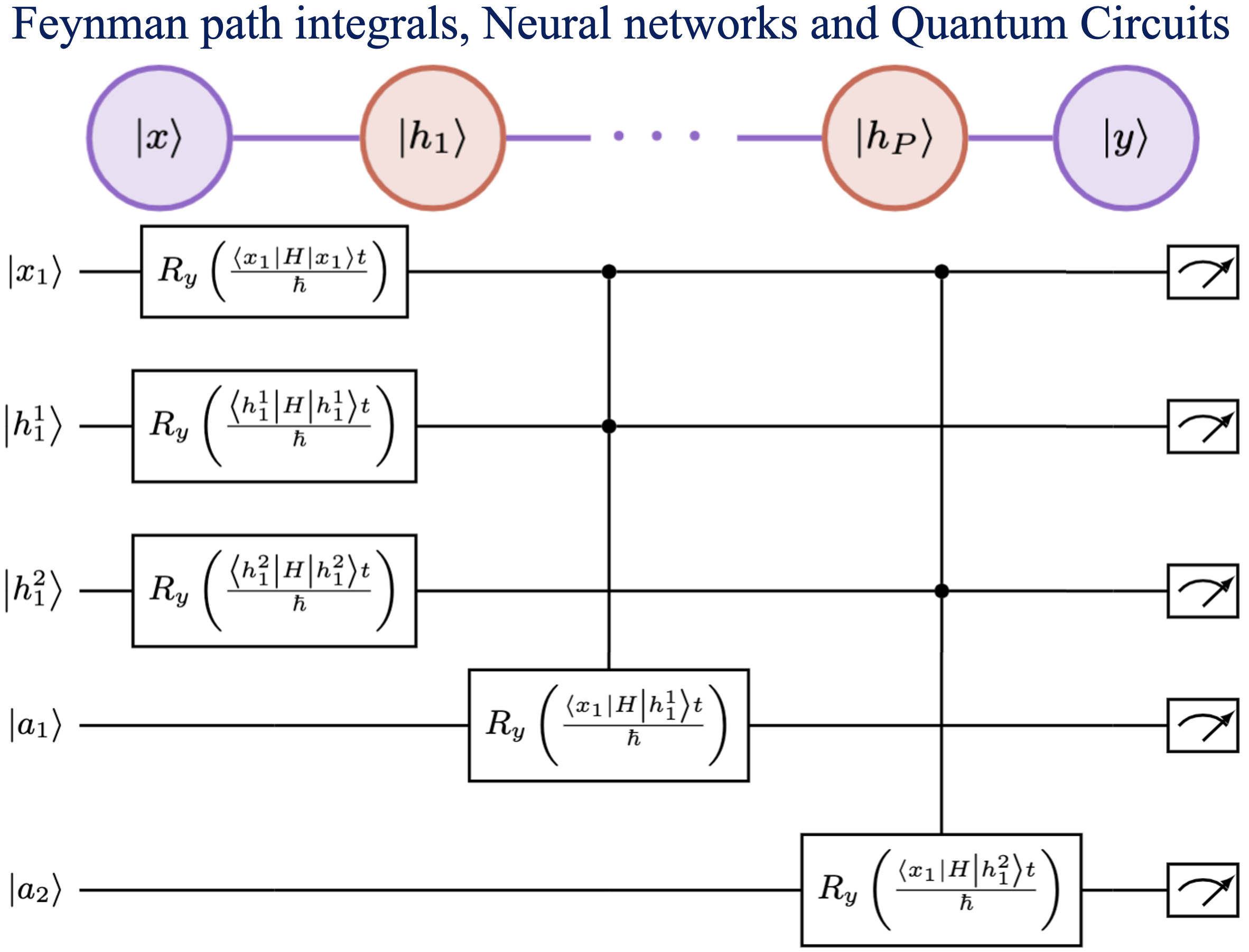Summary: Machine learning has had a significant impact on multiple areas of science, technology, health, and computer and information sciences. Through the advent of quantum computing, quantum machine learning has developed as a new and important avenue for the study of complex learning problems. Yet there is substantial debate and uncertainty in regard to the foundations of machine learning. Here, we provide a detailed exposition of the mathematical connections between a general machine learning approach called Boltzmann machines and Feynman’s description of quantum and statistical mechanics. In Feynman’s description, quantum phenomena arise from an elegant, weighted sum over (or superposition of) paths. Our analysis shows that Boltzmann machines and neural networks have a similar mathematical structure. This allows the interpretation that the hidden layers in Boltzmann machines and neural networks are discrete versions of path elements and allows a path integral interpretation of machine learning similar to that in quantum and statistical mechanics. Since Feynman paths are a natural and elegant depiction of interference phenomena and the superposition principle germane to quantum mechanics, this analysis allows us to interpret the goal in machine learning as finding an appropriate combination of paths, and accumulated path-weights, through a network, that cumulatively captures the correct properties of an x-to-y map for a given mathematical problem. We are forced to conclude that neural networks are naturally related to Feynman path-integrals and hence may present one avenue to be considered as quantum problems. Consequently, we provide general quantum circuit models applicable to both Boltzmann machines and Feynman path integrals.
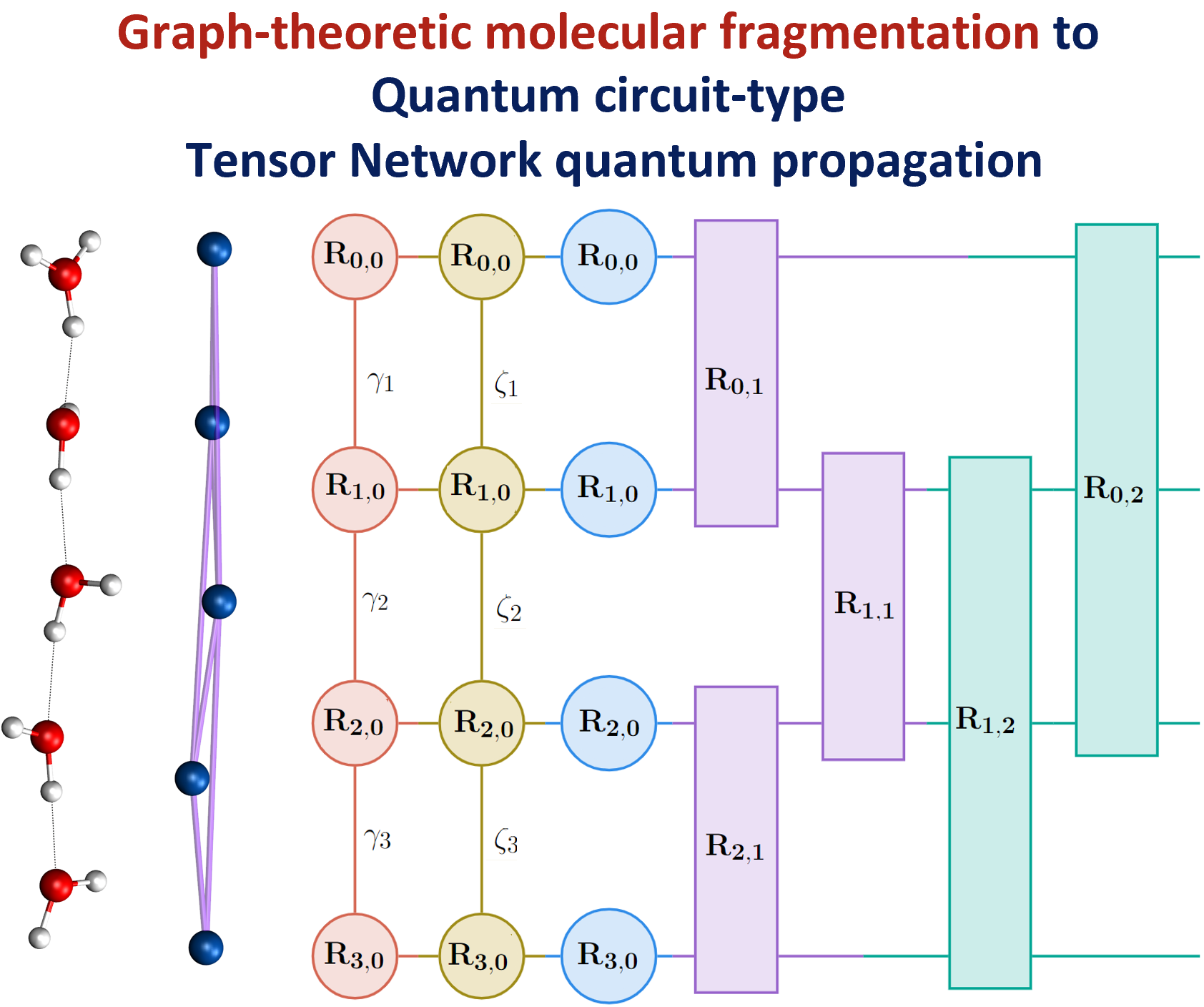Summary: Molecular fragmentation methods have revolutionized quantum chemistry. Here, we use a graph-theoretically generated molecular fragmentation method, to obtain accurate and efficient representations for multidimensional potential energy surfaces and the quantum time-evolution operator, which plays a critical role in quantum chemical dynamics. In doing so, we find that the graph-theoretic fragmentation approach naturally reduces the potential portion of the time-evolution operator into a tensor network that contains a stream of coupled lower-dimensional propagation steps to potentially achieve quantum dynamics with reduced complexity. Furthermore, the fragmentation approach used here has previously been shown to allow accurate and efficient computation of post- Hartree−Fock electronic potential energy surfaces, which in many cases has been shown to be at density functional theory cost. Thus, by combining the advantages of molecular fragmentation with the tensor network formalism, the approach yields an on-the-fly quantum dynamics scheme where both the electronic potential calculation and nuclear propagation portion are enormously simplified through a single stroke. The method is demonstrated by computing approximations to the propagator and to potential surfaces for a set of coupled nuclear dimensions within a protonated water wire problem exhibiting the Grotthuss mechanism of proton transport. In all cases, our approach has been shown to reduce the complexity of representing the quantum propagator, and by extension action of the propagator on an initial wavepacket, by several orders, with minimal loss in accuracy.
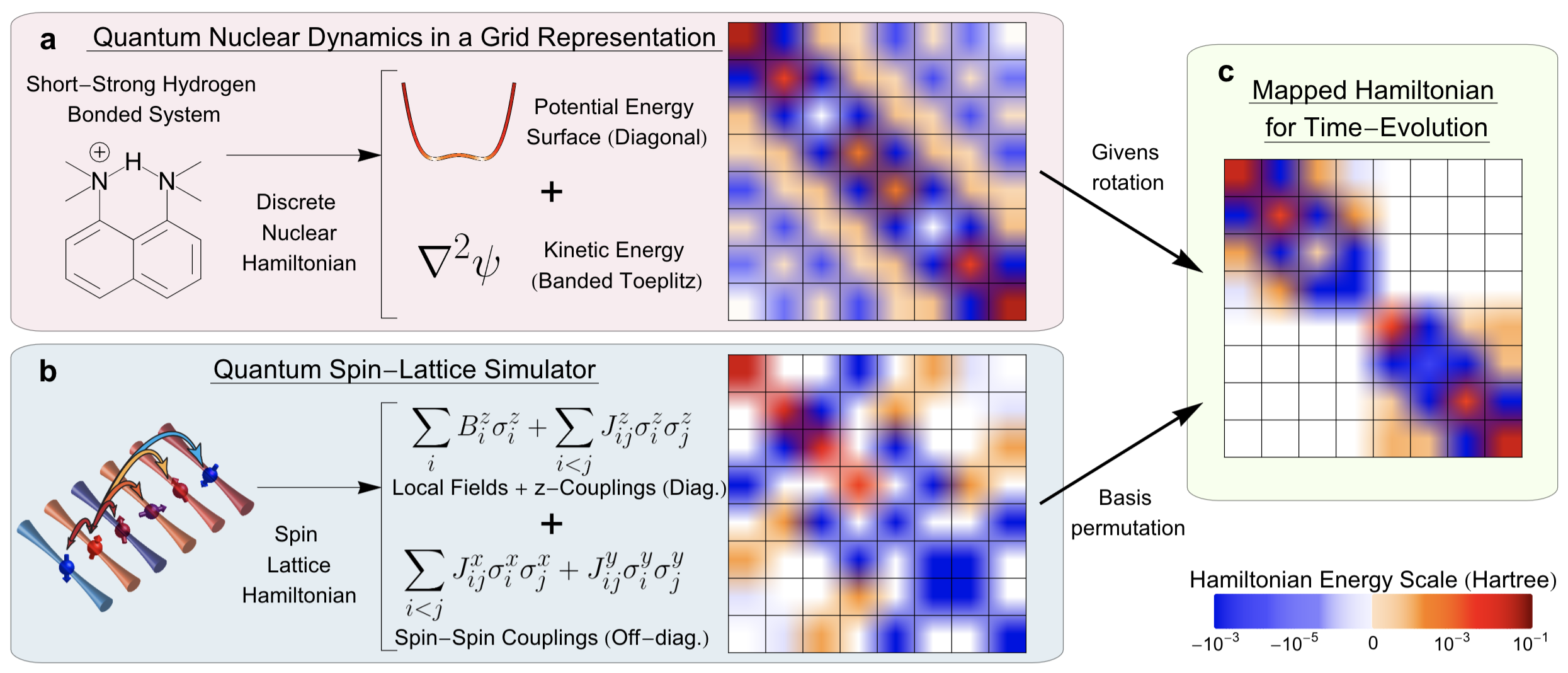Debadrita Saha, Srinivasan S. Iyengar, Philip Richerme, Jeremy M. Smith, and Amr Sabry, J. Chem. Theory and Comput. 17, 6713 (2021).
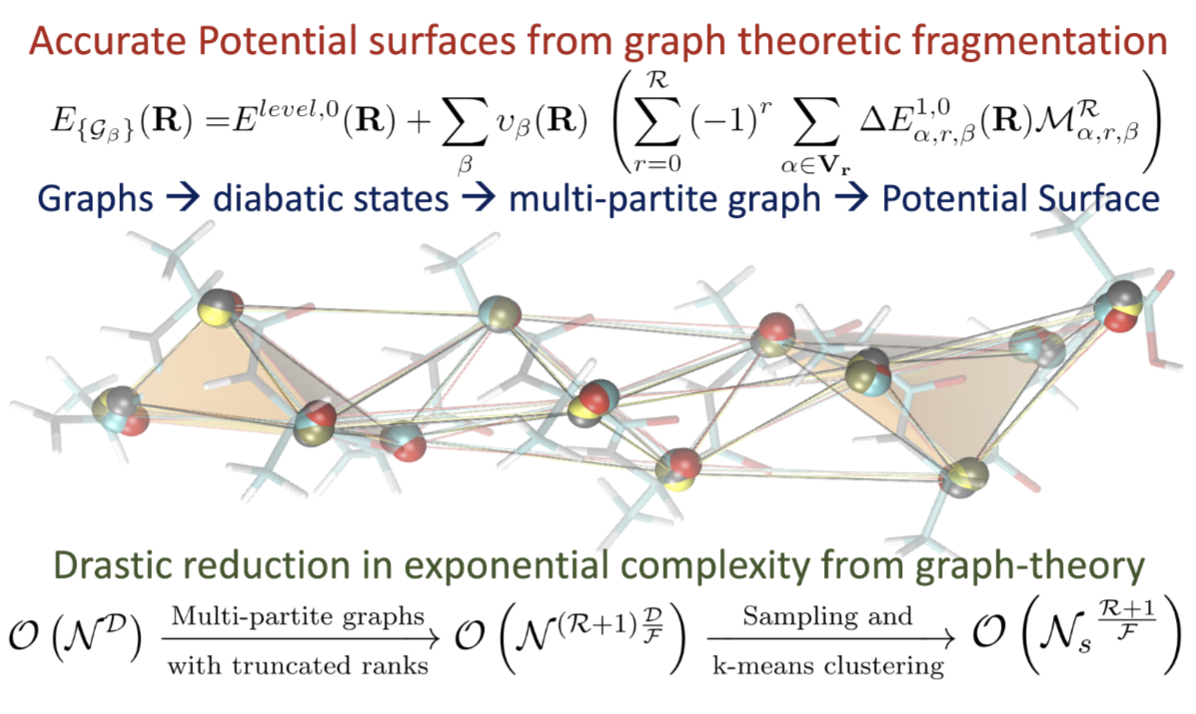Anup Kumar, Nicole DeGregorio and Srinivasan S. Iyengar, J. Chem. Theory and Comput. 17, 6671 (2021).
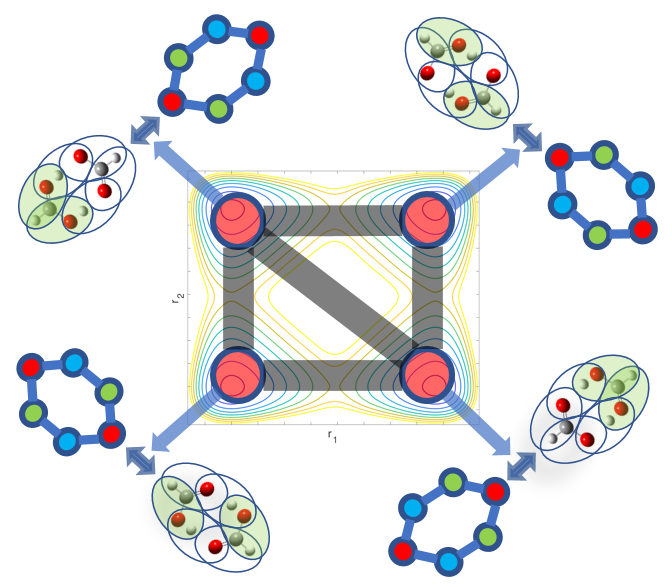A. Kumar and S. S. Iyengar, "Fragment-based electronic structure for potential energy surfaces using a superposition of fragmentation topologies", J. Chem. Theory and Comput. 15, 5769 (2019).
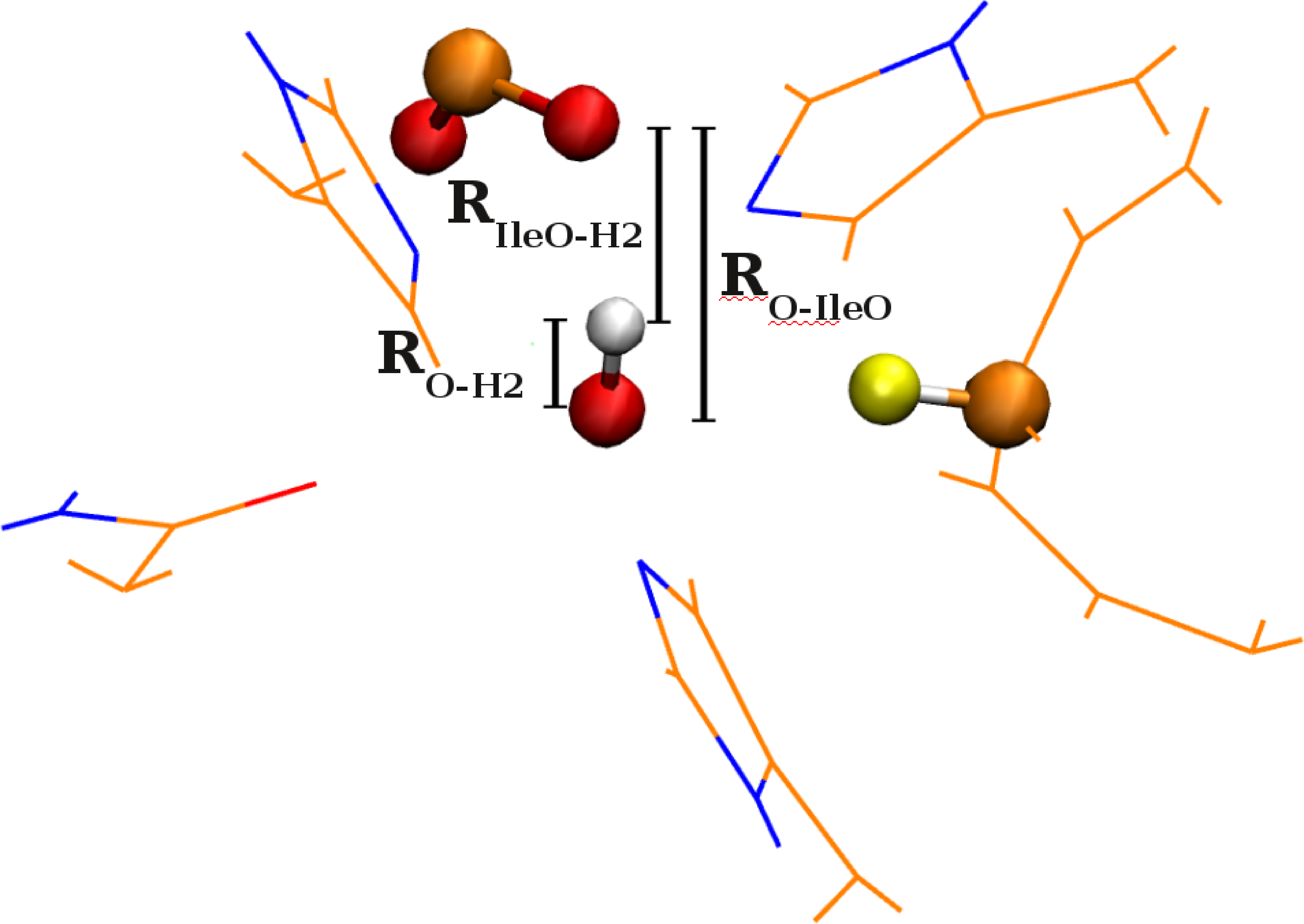N. DeGregorio and S. S. Iyengar, "Challenges in constructing accurate methods for hydrogen transfer reactions in large biological assemblies: rare events sampling for mechanistic discovery and tensor networks for quantum nuclear effects", Faraday Discussions 221, 379-405 (2019).
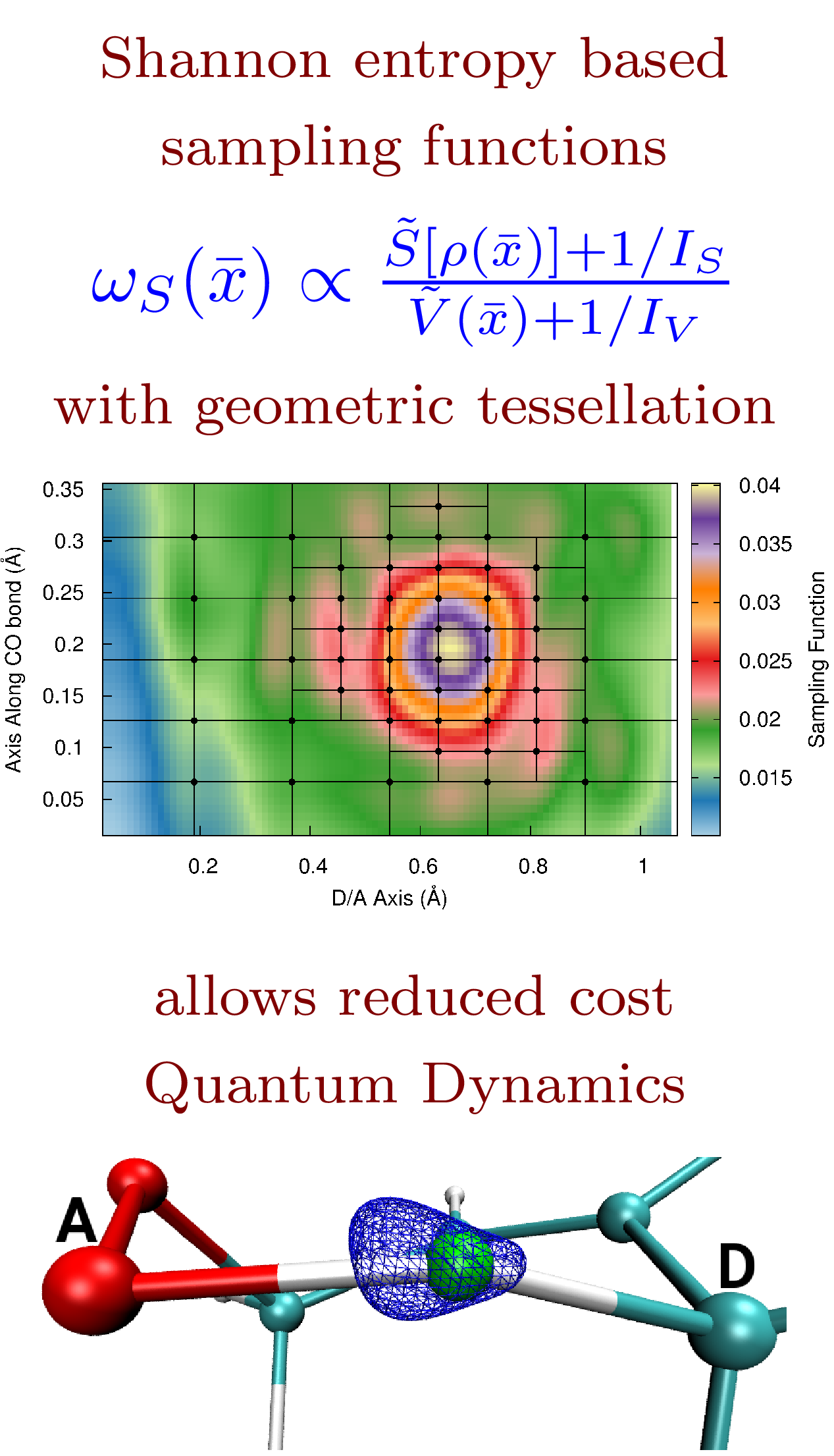N. DeGregorio and S. S. Iyengar, "Efficient and adaptive methods for computing accurate potential surfaces for quantum nuclear effects: Applications to hydrogen transfer reactions" J. Chem. Theory and Comput. 14, 30 (2018).
The College of Arts